KerasでRNN(LSTM)を試してみた

序論

KerasでRNN(LSTM)を試してみました。

以下の記事を参考にしました。（タイトルまでそのまんまじゃないか…）
qiita.com

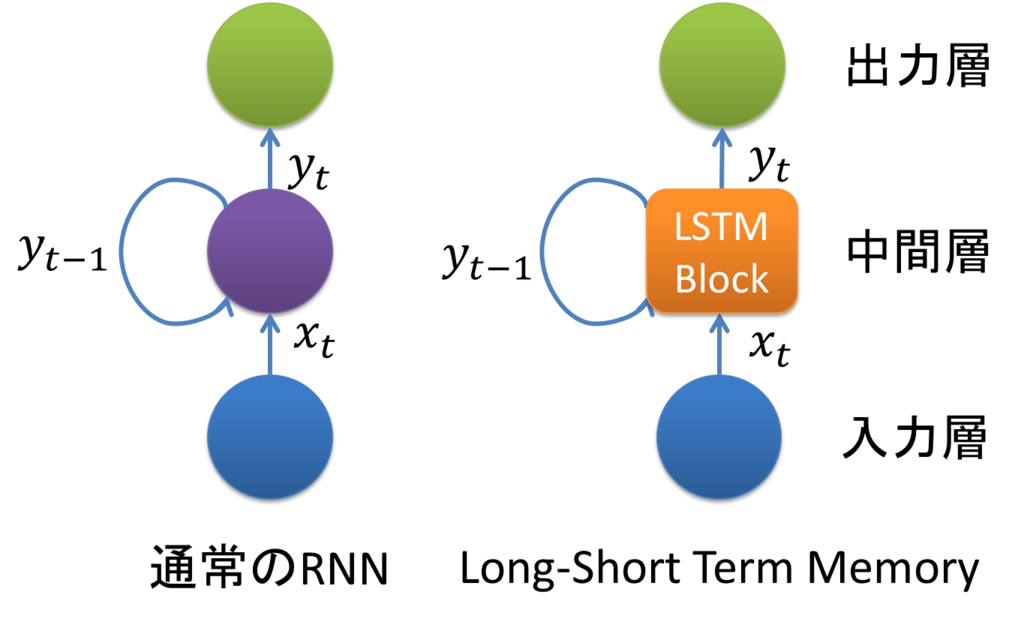
LSTMとは簡単に言うと時系列データを扱えるディープラーニングの仕組みで、RNNの一種です。

LSTM：Long-short Term Memory

従来のRNNでは短期的な時系列相関しか扱えなかったのに対して（比較的）長期的相関を扱えることが特徴です。
応用例としては、為替・株価予測や文章生成、動画の連続的な加工などがあります。
qiita.com

基礎編

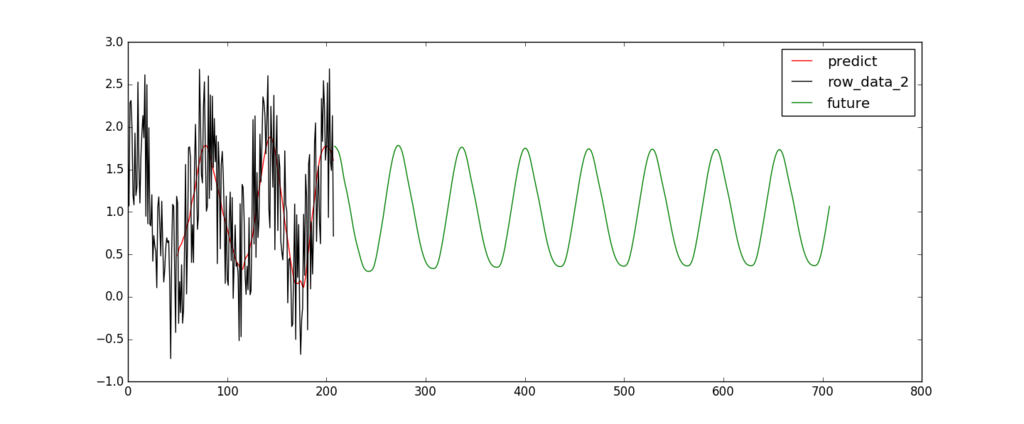
まずは簡単なところとして、連続する数値データから次の値を予測する、というものに挑戦してみます。
ここでは例えば、25個の連続する数値データの入力を得て、26個めの数値を予測するというものをやってみます。

引用元では、正弦波の予測を行っていますが正弦波は簡単そうなのでもう少し難しくしてみたいと思います。

def sin(x, T=100):
    return np.sin(5 * np.pi * x / T)+np.sin(7 * np.pi * x / T)+np.sin(3 * np.pi * x / T)*1.5

これをそのまま学習させた結果が↓

やはり、難易度が上がったようですね。

以前のFFTの記事で触れていますが、正弦波でも周期の違うものを2つ足しあわせただけでも目視では周期を見つけるのは困難になります。
こういったものこそAIの出番ですね（FFTすれば簡単に解析できるけど…）
s51517765.hatenadiary.jp

それと、そもそも波形が難しくなったので目視では振幅以外は合っているのか判断しずらいので、正解波形をプロットするようにします。

f2 =toy_problem(T=500)
plt.plot(range(0, len(f2)), f2, color="k", label="row_data_2") #range(start,end,関数名,)

また、inputデータの長さmaxlenなど、プロジェクトの中で変更しやすいように、引数に設定し整形しました。

学習のepochsは長めに設定しておいて、EarlyStopingで終了させます。

# 学習
early_stopping = EarlyStopping(monitor='val_loss', mode='min', patience=20)
model.fit(g, h, batch_size=300, epochs=300, validation_split=0.1, callbacks=[early_stopping]) #epochsはEarlyStopingによって短縮される

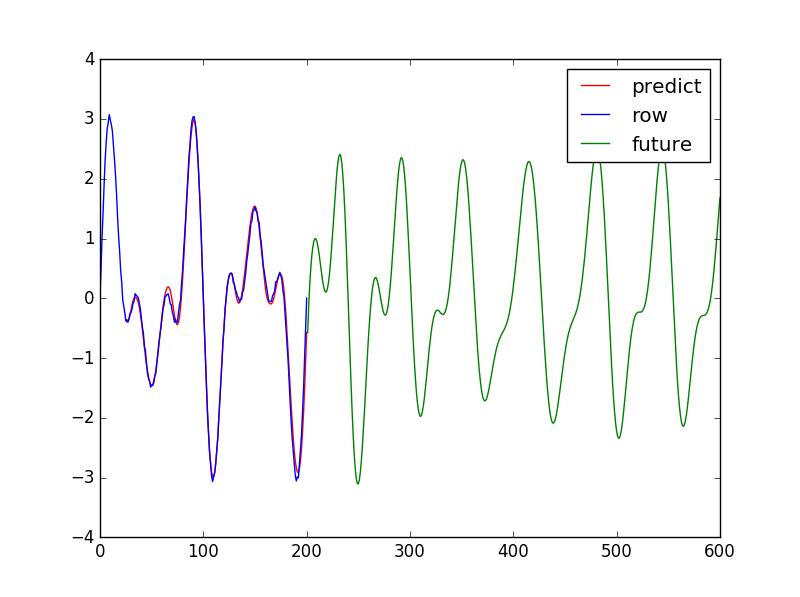
まずは隠れ層やbatch_sizeを小さめにして軽くチューニングすると、短時間でそこそこの出来栄えに持っていけます。これらを大きくすると学習の収束に大変時間がかかるのので、始めにこの辺から手を付けるといいのではないかと思いました。

そんな感じで試行錯誤の結果。

# encoding: utf-8

# https://qiita.com/sasayabaku/items/b7872a3b8acc7d6261bf

from keras.models import Sequential
from keras.layers.core import Dense, Activation
from keras.layers.recurrent import LSTM
from keras.optimizers import Adam
from keras.callbacks import EarlyStopping
import numpy as np
import matplotlib.pyplot as plt


def sin(x, T):
    return np.sin(5 * np.pi * x / T)+np.sin(7 * np.pi * x / T)+np.sin(3 * np.pi * x / T)*1.5
    #return np.sin(5 * np.pi * x / T)


def toy_problem(T, ampl=0.05):
    x = np.arange(0, 2 * T + 1) #等差数列のnumpy配列
    noise = ampl * np.random.uniform(low=-1.0, high=1.0, size=len(x))
    return sin(x,100) + noise #<class 'numpy.ndarray'>


def make_dataset(low_data, maxlen): #maxlenを変更するとグラフがずれるので
    data, target = [], []
    for i in range(len(low_data)-maxlen):
        data.append(low_data[i:i + maxlen])
        target.append(low_data[i + maxlen])

    re_data = np.array(data).reshape(len(data), maxlen, 1)
    re_target = np.array(target).reshape(len(data), 1)

    return re_data, re_target


if __name__ == "__main__":
    inputLength = 50
    TrainingTerm=150
    f = toy_problem(T=TrainingTerm)
    g, h = make_dataset(f, inputLength)
    future_test = g[170].T

    # 1つの学習データの時間の長さ
    time_length = future_test.shape[1]
    # 未来の予測データを保存していく変数
    future_result = np.empty((0))

    length_of_sequence = g.shape[1]
    in_out_neurons = 1 #時刻にたいして出力が１つなので
    n_hidden = 500

    # モデル構築
    model = Sequential()
    model.add(LSTM(n_hidden, batch_input_shape=(None, length_of_sequence, in_out_neurons), return_sequences=False))
    model.add(Dense(in_out_neurons))
    model.add(Activation("linear"))
    optimizer = Adam(lr=0.001) #勾配手法
    model.compile(loss="mean_squared_error", optimizer=optimizer)

    # 学習
    early_stopping = EarlyStopping(monitor='val_loss', mode='min', patience=20)
    model.fit(g, h, batch_size=200, epochs=300, validation_split=0.1, callbacks=[early_stopping])
    #epochsはEarlyStopingによって短縮される
    #batch_size 勾配の更新周期

    # 予測
    predicted = model.predict(g)

    f2 =toy_problem(T=400)

    # 未来予想
    for step2 in range(500):
        test_data = np.reshape(future_test, (1, time_length, 1))
        batch_predict = model.predict(test_data)
        future_test = np.delete(future_test, 0)
        future_test = np.append(future_test, batch_predict)
        future_result = np.append(future_result, batch_predict)

    # sin波をプロット
    plt.figure()
    plt.plot(range(inputLength,len(predicted)+inputLength),predicted, color="r", label="predict") #maxlenのぶんオフセットしたところから
    plt.plot(range(0, len(f2)), f2, color="k", label="row_data_2") #range(start,end,関数名,)
    plt.plot(range(0+len(f), len(future_result)+len(f)), future_result, color="g", label="future")
    plt.legend()
    plt.show()

応用編

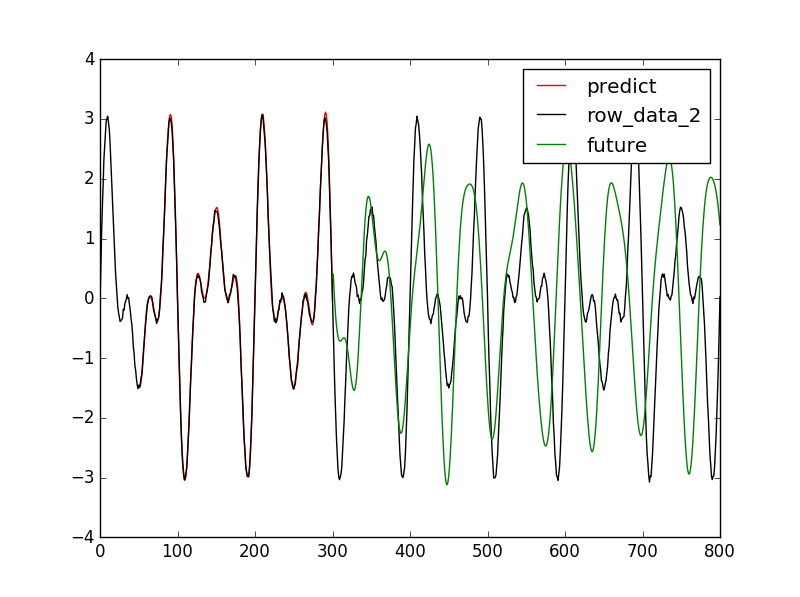
株価や為替のデータはcsvなどで提供されているようなので、このようなデータを取り込む練習です。
基本は正弦波ですがこれに大きめのノイズを足してみました。
これを先ほどのLSTMモデルに学習させます。

def import_text_to_np():
    file = open('test.txt', 'r', encoding='utf-8')
    line = 1
    list =[]
    lineall = ""
    while line != "":
        r=random.random()
        line = file.readline()
        line = line.replace("\n", "")
        # line=line.replace(("\ufeff",""))
        try:
            line = float(line) *0.8+r*2
            list.append(line)
        except:
            print(line)
    print(type(list))
    print(list)
    list=np.array(list) #listをnumpyのlistに変換   https://note.nkmk.me/python-numpy-list/
    print(type(list))
    print(list)