科学・技術界隈にかかわっているとデータ解析で出てくるFFTですが、なかなか計算するのは複雑でしかも、それが正しく計算されたのかが、わかりにくいところがあります。
そこで、今回はFFTがだれでもそこそこ使えるようにまとめてみました。
FFTとは
あらゆる周期関数は正弦波の足しあわせで表現できるという特性を利用し、周波数成分に分解すること。これは、フーリエ級数展開を数値的に計算しているのと同じことになります。
これをなるべく少ない計算量で行うのが”高速”フーリエ変換です。
どのような目的で使うの?
工業的にはノイズ(音や振動)の発生源の特定のために使われます。音というのは周期振動によって発生するものであり、その本質はなにかしらの機械的振動が空気中に広がっていくものです。
よって、その音であったり振動をFFTすることで周波数を特定すればそれに相当する回転数をもった部品が原因であると特定できます。
音の場合はマイクで拾ったものを電圧として受信し、振動であればAEセンサなどで拾ったものを電圧として取得します。
計算方法は?
いつくか方法がありますが、もっとも一般的なのは ”Cooley-Tukey のアルゴリズム” を利用したものです。このアルゴリズムによって、計算量は O(N2) から O(N log N) まで落とせるが、制約として入力は2^n個(4,8,16,32,64,…)でなければならない。この制限下でのみ計算量を削減できるアルゴリズムです。
Cooley–Tukey FFT algorithm - Wikipedia
実際に計算してみる
適当な周期関数として時間に対して2つの正弦波をたしあわせたものをFFTしてみます。図の下のグラフがもとの正弦波で上のグラフがそれを足しあわせたものです。
下のようなグラフが出てくれば、深く考えなくても周期を見つけることは簡単ですが、たった2つの正弦波が足しあわされた(混ざった)だけでこれほど複雑になり、周期を見つけることは大変難しくなります。

sin(time /10*1000)+sin(time /17*1000)
適当に作った周期関数ですが、そのもととなる正弦波の周期(周波数は)以下のようになります。
| 周期(s) | 0.0628 | 0.1068 |
| 周波数(Hz) | 15.915 | 9.362 |
これが数値として得られているとして一般的に↓のように得られます。

これをFFTした結果が、こちら。

サンプリング数を2水準で実施してみました。
512ポイントでは二つのピークを検出できていますが、128ポイントではそのピークがくっついてしまい、15.625Hzは何となく肩がありますが、9.362Hzはかなりずれたところにピークがあります。また、サンプリング数によって大きく周波数が変わっています。
これは、サンプリング数により周波数の分解能が違うためです。
もっと厳密にいえば、512ポイントでも15.915Hzは15.625Hzであり、9.362Hzは9.766Hzと算出されています。
15.915Hzはたまたま検出可能周波数として、15.625Hzがあったため近い値が出ましたが、9.362Hzはもっとも近いのが9.766Hzであるためこのようにずれて算出されます。
検出可能周波数
下図は1kHzのサンプリング周波数のときの検出可能周波数です。右方向がサンプリング数になります。
9.362Hzについては±0.1Hzが出るには2048ポイントが必要ということになります。
(もちろんサンプリング周波数によってもかわります)
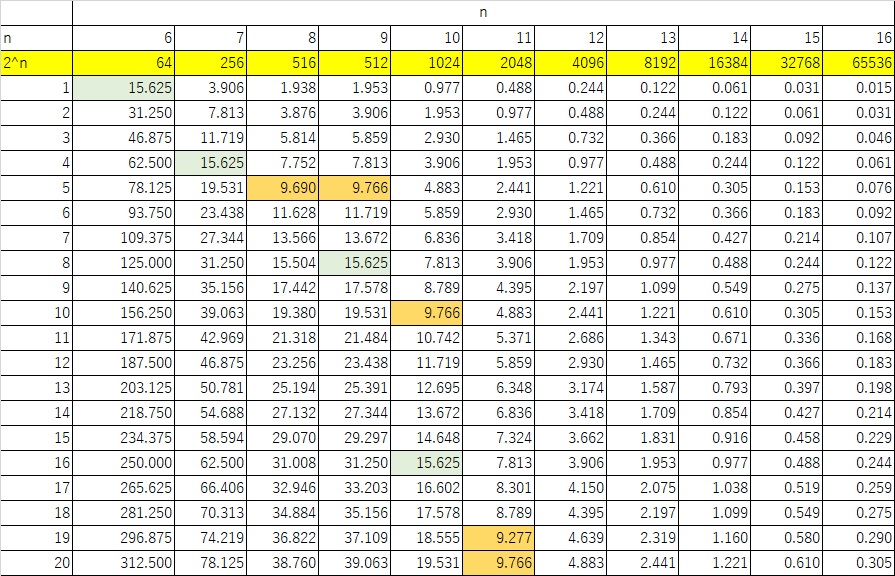
ちなみに小数点以下2桁が一致するには32768ポイントのサンプリングが必要になります。

まとめ
FFTは簡単に周波数解析ができますが、その分解能についてよく理解しないで使おうとすると、その周波数が誤って認識されてしまいます。あくまでも簡易的な解析ができるだけでありますが、サンプリング数を十分に増やしていけばかなりの(精度)分解能が得られます。
ですがFFTとは言っても計算量はO(N log N)で増えていきますので、その計算時間はそれなりになります。
また、ピーク強度がこの計算方法では入力データ数によって異なります。ピーク強度は相対的な比較になることにも注意が必要です。
ツールのダウンロード
csv形式のデータソースからFFTを計算するツールを作成しました。ライセンス認証によって1048576データ(Excelの最大行と同じ)までの入力に対応します(計算時間はかかります)。
無料でも128データまでの解析・計算ができます。
www.vector.co.jp